De Morgans Law: (flip Us is true) , image of set: [min,max] ; one-to-one: horizontal line test; Onto: Image must equal domain; Bijective: 121 and Onto; 

|| EV ||

Possible outcomes: repetition formula = n^k ex: 5 awards(k)  30 students(n), no limit to awards per student.|| permutation formula = P(n,k) = n! / (n-k)! ex: student gets 1 award, so students decrease by one each award. ||

no overlap probability = P(n,k)/rep formula || Arrangements: a=slots -> a! can be multiplied by arrangements within slots || die sum prob: list combos that lead to sum for each (die rolled multiple times means each combo has rolls! perms), add up perms, sample space in this case is 6^n rolls so perms/sample space = Pr || Grid problem: List total movements ie: ups and rights, # paths is = to total! / U!*R! ; cross thru point: paths to point times paths from point || 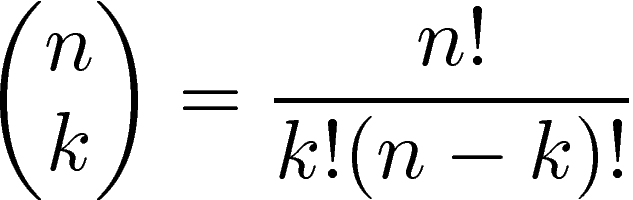Students in class prob: even stud dist g per class-> Class A, B, C; k studs of interest; class pop n; Pr interest all in class A (n - k choose g- k) / (n choose g) ; Pr interest all in any class num class * previous || 

Events: Ex: events E,F,G; at least 1 event occurs=EUFUG ; at least 2 occur=(E∩F)U(F∩G)U(G∩E); none occur=E^c ∩ F^c ∩ G^c ; at most 2 occur = (E∩F∩G)^c ||

Ex: Students in a class, 60% love coffee, 70% chocolate, 40% both; prob that random selection is neither; P(A)=.6, P(B)=.7, P(A∩B)=.4 ; interest in P(A^c ∩ B^c) can be found using demorgans = 1-P(AUB) = 1-(.6+.7-.4) = .1 || Ex: six sided loaded die, even face 2x likely; prob model for 1 roll; find prob that outcome less than 4; determine probs x= P({1}) = P({3}) = P({5}), y= P({2}) = P({4}) =P({6}); y = 2x; Axiom 2/3 -> 1=P{1-6} = 3x + 3y = 9x =1; x= 1/9 ; y= 2/9; P(1,2,3) = 4/9 ||

Ex. Prob of winning dice toss is q, A starts and if he loses, dice is passed to B who attempts to win. continues back and forth until one wins; what are respective probs of win? -> P(Awin) = sum(k=0, inf) (1-q)^2k * q; geo-sum ; P(Awin) = 1/(2-q), P(Bwin) = 1-P(Awin) = (1-q)/(2-q) || Comm system: P(good con) = .8; P(bad con) = .2; Error in trans P(error|good) = .1; P(error|bad) = .3; P(good trans)?; P(E^c) = P(E^c|G) * P(G) +P(E^c|G^c) * P(G^c) = .9*.8 +.7*.2 = .86

(E∩F)∪(F∩G)∪(G∩E)(E∩F)∪(F∩G)∪(G∩E)